How are Runs Really Created
By Tangotiger
Part 1 - Forget what you know
Run estimator, run estimator, here, there, and everywhere
Every week, someone comes out with a new run estimator. You know those right? Take various components, like hits, HR, walks, outs, apply some constant to each of them, or maybe multiply and divide these components in some fashion, and the result is the runs a team was expected to score.
Let's take the basic version of Bill James Runs Created: take the Total Bases and multiply it by the On Base Average and you get Runs Scored. So, in a 9 inning game with 15 total bases, and you have 13 of 39 batters safe, that gives you an expected 5 runs scored. And if you look at a large enough sample, a team with 15 TB and a .333 OBA will probably score around 5 RPG. So, what's the problem?
The problem is that this does not model reality. If you add a single to this game, you get 16 TB, a .350 OBA for a total of 5.6 RPG. That extra single added .6 runs to this game. Sounds about right, no?
No. Pete Palmer's Linear Weights says that an average single will add .47 runs to a game. Gee, that sounds about right, no?
No. The problem with these run estimators (and all their offshoots and close family members like Extrapolated Runs and Equivalent Runs) is that they don't model reality. The provide an ESTIMATE based on a formula that they hope capture reality. They don't.
Modeling Reality
How can we show this? What does model reality? How can we take any system (not necessarily baseball), and create a model? The best way is to determine all of your known variables, allow some allowances for unknown variables, and create a simulator that uses every variable you know and how each variable interacts with each other. (Think flight simulators.)
Ok, hot shot. So, how much run value does a simulator say a single is worth?
If you were to construct your model perfectly (or as close as possible), you can create a system where 15 TB and a .333 OBA will produce 5 RPG. That is your controlled environment. If you then add a single randomly inside this system, one variable, and look at the result, you will conclude that the effect of adding that variable resulted in a change in the output of the system (over a large enough sample cases). In this case, adding a single would add .48 runs in this game.
Ok, so a single is worth .48 runs. Linear Weights is better, right?
Wrong. What that .48 means is that the MARGINAL effect of the single to a SPECIFIC run environment has a positive run effect of .48 runs. If you had a different run environment, say like the one Pedro or Randy provide their opposition, a single will not add .48 runs. It'll be more like .38 runs. This again can be shown with a perfectly constructed simulator.
Even worse, adding TWO singles does not necessarily add .96 runs, nor does adding 100 singles add 48 runs. Baseball run construction is non-linear interdependent.
But do we have to run a simulator every time? Isn't there some relationship that we can find that'll show us that it's .38 or .58 or whatever?
Yes. And for that we have to understand how runs really are created.
An Interlude
Bill James has made several modifications to his basic Runs Created. These changes were made to better capture reality. Actually, they were made to improve accuracy over a sample of team totals. The changes made are good overall, but he makes one glaring error. While James has the correct basis for capturing the model of interdependence and non-linearity (on a team level anyway), this one error is his downfall.
Pete Palmer strangely enough showed us the dynamic values of each hitting component by era in his book The Hidden Game of Baseball. However, he took the easy way out and decided to use static (non-changing) values for the positive hitting components, and applied a dynamic (changing) value only to the out component. This gives the impression that hits and HR and walks have static values regardless of run environment, while the out is the only one that changes. The easy way out is not only the wrong way out, but it doesn't even capture reality.
Part 2 - Using a little common sense... and some math
Runners on, and runners over
Runs are created by getting runners on base, and moving them over. Most people look at the OBA as the first part, and the SLG as the second part. And the combination of the two should generate runs scored. It's not that simple.
Using common sense on an uncommon example
Have you ever played in a softball league where the typical team scores upwards of 20 runs in a 7-inning game? Such a team will send say 51 batters to the plate, 21 of which will be out, and 20 of the other 30 batters will score. If a runner that gets on base will score two-thirds of the time, how much more valuable is the home run compared to a single? In softball, because the run environment is so high, it is important just to be able to get on base, because you know that you have a good chance at scoring.
Take an even more extreme example. Imagine playing in a run environment with 100+ runs scored in every game. 90% of the baserunners end up scoring. In this environment, there is very little difference between a home run and a single. Just by virtue of getting on base, you are bound to score. There is far more value in getting on base, than of moving runners over.
Take an extreme example the other way. Pedro Martinez provides his opposition with a very low run environment. Getting on base is not enough. Very few of those runners will end up scoring. However, if you can hit a home run, you will be adding alot of run potential to the runners on base. Not only that, but when you hit a home run, you are always guaranteed 1 run.
The run value of various hitting events
Here is what our common sense tells us, in graph form.

This however is contrary to what Bill James' Runs Created tells us. If you have a formula that says TB x OBA, then this implies that you have an always-rising value for each hitting event. Suppose that you have 100 total bases in a game, and the OBA is .800 (40/50), for a total of 80 runs. If we add 1 HR to this system, that gives 104 TB, and an OBA of .804, for a total of 83.6 runs. This one HR is now worth an astonishing 3.6 runs! But common sense has shown us above that this is wrong.
This is what Runs Created tells us, in graph form.
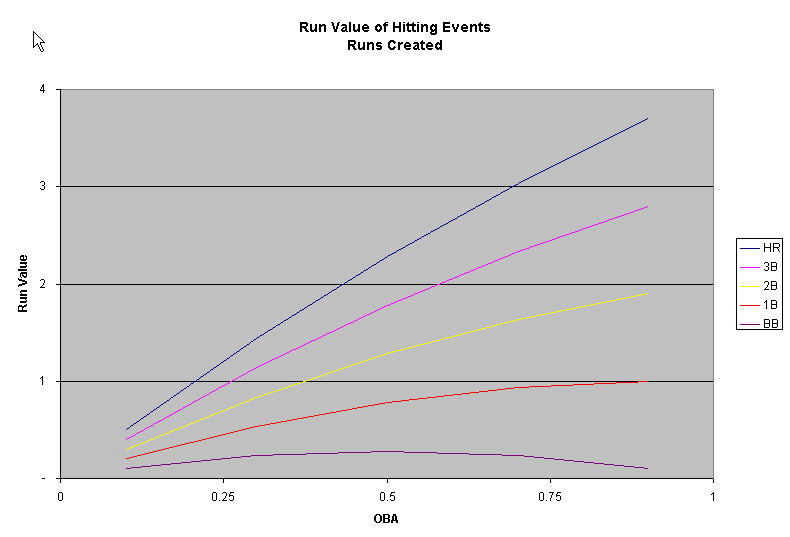
What is very important to note at this point is that if we concentrate at the above two graphs between the OBA points of .300 to .400 (where MLB teams perform in reality), we see that Bill James' Runs Created does conform somewhat to what we perceive as common sense. However, the reason that Runs Created "works" is not because of its construction. It's purely an accident that it works. It just so happens that the points at which Runs Created and common sense intersect is exactly at the same points at which MLB teams play at!
Furthermore, note that what applies to teams does not apply to individuals. Individuals need their own run construction formula.
Don't like common sense? Let's try some math
Based on my analysis of the play-by-play data from 1974 to 1990 provided by Retrosheet and software provided by Ray Kerby, here is the likelihood of a runner scoring, based on which base he is on, and the number of outs
Chance of scoring, from each base/out state 0 outs 1 out 2 outs 1B .38 .25 .12 2B .61 .41 .21 3B .86 .68 .29
This simply means that if you have a runner at 3B with 0 outs, then he has an 86% chance of scoring (that's the "getting on base" value). If someone can drive him in, that batter will add .14 runs (to the already established .86 for a total of 1.00; this is the "driving him in" value).
As you can see the higher the chances of scoring, the less value there is in driving in a runner. Let's look at the run-driving value of the walk.
Run Driving value of the walk, from each base/out state 0 outs 1 out 2 outs 1B (to 2B) +.23 +.16 +.09 2B (to 3B) +.25 +.27 +.08 3B (to home) +.14 +.32 +.71
Obviously, the most valuable walk in terms of moving runners over is the walk that scores the runner from 3B and 2 outs. This happens rarely, as the bases would be loaded. So, on top of this table, we need a "frequency" table that shows how often a walk occurs in each of the above scenarios.
Frequency of walk in moving runners over, from each base/out state 0 outs 1 out 2 outs 1B (to 2B) 0.053 0.084 0.114 2B (to 3B) 0.012 0.027 0.042 3B (to home) 0.002 0.006 0.010
As you can see, walks are not given out in random fashion. A large portion of them occur with 2 outs, when they do the least damage. Multiplying these two tables will give you the "moving over" value of the walk. This works out to +.06 runs.
The "getting on" value of the walk can be determined using the "chance of scoring" table presented above, with the appropriate frequency at which walks occurs in those states.
Frequency of walk occuring, by outs 0 outs 1 out 2 outs 0.316 0.326 0.359
Doing a similar multiplication, and we see that the "getting on" value of the walk works out to +.24 runs. The run value of the walk is therefore equal to +.30 runs.
We could have performed this analysis in several other ways, each of which would yield the same result of +.30 runs. One is to look at the run expectancy (RE) before the walk, the RE after the walk, take the difference, add the number of runs that score, and you get the run value of the walk. Doing that and we get a run value of +.30 runs. Another way is to construct a simulator, insert a walk, and look at the difference. You will find that given the run environment of 1974-1990 you will get a run value of +.30 runs.
The important point to remember is that the run value of all the hitting events is dependent on the run environment. The walk is worth more today than in 1968. It is worth more in Coors than at the Astrodome.
Using the RE approach, here is the run values of all offensive events.
Run values, 1974-1990, using the RE approach Single Double Triple HR Walk IBB HBP Reached Base On Error Interference OtherSafe 0.460 0.750 1.033 1.402 0.303 0.176 0.330 0.478 0.357 0.631 Sac Strikeout Out (0.090) (0.269) (0.265) SB CS Pickoff Pickoff Error Balk PB WP DefensiveIndiff OtherAdvance 0.193 (0.437) (0.228) (0.182) 0.250 0.276 0.278 0.132 (0.362)
Another Interlude
Remember what the run values represent. They represent the MARGINAL effect of the offensive events GIVEN a specific environment. Remember that. Repeat that.
If you get an out in a run environment that scores 3 runs per INNING, that is very costly to your team. It has a negative effect only because of the expectations of future runs. The out is not very costly when Bob Gibson's 1.12 ERA is on the mound, simply because the expectation is low that a run would be scored at all. -.27 runs doesn't mean that you will score negative runs, but rather that your team's run potential has been decreased by .27, GIVEN the environment in which the out was created.
I will talk more about how to understand the out in the frame of reference of Runs Created and Linear Weights in my next article. And I will apply David Smyth's BaseRuns, a constructor that models reality in almost all run environments.