
Aging Patterns
by Tangotiger
What is a player's peak age? What does that even mean? Is it the single year where the player has his best year, or is it the midpoint of number of years where the player has the best part of his career? As with anything, you have to define the question before you determine an answer. Some analysts even come up with an answer first, and then construct the question. I used to do this. Tim Raines is my favorite ballplayer ever. And I would always argue he was the best, using anything I can find to substantiate that argument. I did the same thing in hockey when comparing Bryan Trottier to Wayne Gretzky. It took me a few years to realize that I was wrong on that one.
Note: Age is calculated as of July 1st, with the remainder rounded off. It doesn't really matter how you calculate age, as long as you calculate it the same way for every player. Every other analyst uses a player's age as of July 1, and drops off the remainder. For example, Tim Raines was born 09/59. In 1999, I have him as 40 years old, while the other analysts mark him as being 39. In actual fact, Raines was 39 years and 9+ months on July 1, 1999. While other analysts truncate his age to 39, I round it to 40. The reason I do this is that the "age 40 class" represents the players who are between 39.5 years and 40.5 years old, and therefore will average 40.0 years old. I don't see any reason to truncate ages, when every other number manipulation we do uses rounding. In any case, no big deal, as long as everyone is consistent within their study.
Defining a peak age
Let me first define a peak age. A player's peak age is that age which shows the most evidence that a player's abilities is at its highest. Now, what do we use as evidence? A baseball player's statistics is the most objective data we have to make this determination. But are the stats themselves misleading in any way?
Lies, damned lies, and statistics
You have to search for the truth in stats. If a player hits 30 HR in 600 AB, is his ability to hit 1 HR every 20 AB? If a player hits 3 HR in 60 AB, is his ability to hit 1 HR every 20 AB? What those 600 AB represents is a sample of a player's abilities. The higher the number, the more indicative the sample is of the "population". If it was humanly possible, researchers would love to have a batter come up to bat in game conditions 100,000 times in a 1 year span. Since this is not possible, you have to take what you're given, and start applying confidence levels.
This is just like an opinion poll. You sample 1,000 people, and declare the results of the poll to be accurate within 3 percentage points, 19 times out of 20. A player's at bats is simply a sample poll of his abilities. The higher the sample, the more confident you are with the results, and the more accurate the results are.
How do the pollsters come up with such a statement? It's all based on distributions and probabilities. Suppose "p" represents the probability that something is true, and "q" is the opposite (or 1 minus p). The number of samples is represented by "n". To calculate one standard deviation, you simply take SQRT(p x q / n). In this poll example, it might be SQRT(.5 x .5 / 1000) = .016. One standard deviation means that 68% of all results will fall within .500 +/- .016 probability. Two standard deviations is +/- .032, and you expect 95% of all samples to fall within this range.
So, is it enough to just look at a player's season and declare something about his abilities? Well, let's look at a player's batting average. Suppose a player hits .300 in 600 at bats. Is his true talent level really a .300 hitter? Well, we can say that 95% of the time, we expect a .300 hitter to have a batting average of about between .260 and .340 in 600 at bats. We can also say that 95% of the time, a .270 hitter will hit between .230 and .310. So, we can't say for sure how good a hitter this player is, with a 600 at bat sample. But how about after 10 years? What if he hits .300 with 6000 AB? Well, now we can say with 95% certainty that this player is a .290 - .310 hitter. The more we can sample the player, the more confident we are.
Looking for aging patterns
A simple technique to look for aging patterns is to simply start adding up the number of hits a player has at every age. Do this for all ballplayers, and you get an aging pattern. The first problem with this is that you have more players who play at the age of 28 than at the age of 38. Just by the sheer volume, it looks like a player will peak at 28 rather than 38.
A second technique is to look at the average at each age. This should take care of the volume problem of the previous technique. Except now, if you look at a pitcher's K/IP rate for all pitchers of age 45, it looks like a pitcher has a pretty good rate at that age. The problem here is that while Nolan Ryan makes up a tiny part of the age 28 class, he makes up a huge part of the age 46 class. Each class is represented by different players. Therefore, the difference is not only attributed to the age, but to the sample chosen.
A third technique is the delta approach. You take a group of hitters who all had at least 300 PA at age 32 and at age 33. You figure out the batting average for this sample group of players for each of the two years. Since your sample is probably quite large, you expect that all the outside conditions that could affect the results will "cancel out". The only difference between these two groups of exactly the same players is the age. Therefore, if this sample of players hit .276 at age 32 and the same group of hitters hit .273 at age 33, we can say, with reasonable certainty, that a hitter's performance will diminish by .003 batting average points between the ages of 32 and 33. You do this matched pair set for all years, and you end up getting a chain of "deltas" (or differences). Then, you can say something like, a .260 hitter at age 23 will hit .265 at 24, .270 at 25, .273 at 26, .274 at 27, .274 at 28, .273 at 29, .271 at 30, etc., etc.
I've used this last approach many times. But are there limitations to such an approach? Unfortunately, yes. The problem is that you are selecting players with 300 PA in year x, and in year x+1. Just by the virtue of them having 300 PA in the year in question (year x+1) automatically means that they probably had a decent year. Therefore, it is not a random sample. It's rigged. This is called selective sampling. If we decided to just take all the guys with 300 PA in year x, and see how they did in year x+1, then what do you do with the guys with 32 PA in year x+1? We are not very confident in what the performance of 32 PA represents. What you can try to do is weight the performance by the lower of the 2 PAs. This way, a guy with only 32 PAs won't affect the results much. But again, this reintroduces the previous problem. By virtue of having only 32 PAs probably means that this player did not have a good year to begin with. (I realize that there are many reasons that a player can go from 300 PA to 32 PA. Injuries being one, poor initial performance being another, etc. If you look, you will see that the overall performance of players who go from 300 PA in one year to 100 PA in the next year will show a drop in production. Whether this means a drop in ABILITY is not implied.) We've got problems.
Therefore, what we have to do is measure the degree of this problem. A limitation exists, but how bad is this limitation? And is this limitation different for hitters and pitchers?
Looking at different samples
If you look at all players who played exactly two seasons at age 24 and 25, what do you think you will find? Well, first of all, if he only played two seasons, then he probably wasn't very good. Or more precisely, he probably didn't put up good numbers, because all he had to show was a sample of his true ability. Secondly, if he was good enough to get a look at a second season, but not good enough to get a look at a third season, then chances are that his second season was worse than his first. Therefore, when you select your group of players, you have to be aware of this.
The study
I will define a regular player as someone who has at least 300 PA (AB+SF+BB+HBP)
in a season. I will look only for players who had an uninterrupted string of
regular seasons (meaning that Ted Williams is out of this study, but guys who
were part-timers at the start or end of their careers like Tim Raines are in).
I also only look at players whose first regular season was no earlier than 1919
and whose last regular season was no later than 1998. From this group of players,
I will break them down by
- debut year as a regular
- number of years as a regular
I will also use a hitting measure I "invented" called Linear Weights Ratio (LWR), which you can consider as a total hitting measure. (The formula for this study is: 1 x 1B + 1.6 x 2B + 2.2 x 3B + 3.0 x HR + 0.7 x BB + 0.7 x HBP all divided by AB - H + SF)
For each player, I express each of his seasonal LWR as a percentage of his career-high LWR. Therefore, every player will have a 100% level at some point in their career. I'm trying to determine a player's "% of peak" for every year.
Concentrating only on those players that debut at age 25 and who played for 9 years, here's what this gives us:
Debut age 25, 9 years Age Peak% 25 0.844 26 0.844 27 0.836 28 0.875 29 0.842 30 0.804 31 0.871 32 0.824 33 0.794 The total number in this sample is 15 players
So, what does this tell us? Well, the players hit their peak, on average, at age 28, followed closely by age 31. Their 3 worst years were at age 30, 32, 33.
Now, what do we learn here? First of all, their worst year was their last year. This is practically a given in any sample that we will see. Chances are a player's skills did diminish, but probably not as much as the stats said they did. A team though will ignore that, and simply not give that player a chance.
Here's the table showing all players who debut at age 25, broken down by years of experience. The last line in each table is the number of players in the sample.
Peak%, players debut age of 25, by years of experience Age 2 3 4 5 6 7 8 9 10 11 12 13 14 15 25 0.950 0.886 0.900 0.887 0.907 0.822 0.833 0.844 0.811 0.780 0.848 0.842 0.753 0.806 26 0.935 0.968 0.896 0.874 0.881 0.882 0.872 0.844 0.821 0.849 0.828 0.969 0.880 0.765 27 ----- 0.865 0.939 0.840 0.849 0.872 0.882 0.836 0.894 0.919 0.807 0.856 0.926 0.775 28 ----- ----- 0.851 0.811 0.897 0.879 0.866 0.875 0.893 0.876 0.831 0.862 0.897 0.784 29 ----- ----- ----- 0.841 0.868 0.810 0.905 0.842 0.865 0.915 0.799 0.895 0.805 0.823 30 ----- ----- ----- ----- 0.785 0.826 0.875 0.804 0.840 0.895 0.756 0.845 0.853 0.915 31 ----- ----- ----- ----- ----- 0.774 0.851 0.871 0.818 0.973 0.808 0.928 0.992 0.763 32 ----- ----- ----- ----- ----- ----- 0.779 0.824 0.842 0.879 0.818 0.888 0.840 0.909 33 ----- ----- ----- ----- ----- ----- ----- 0.794 0.771 0.866 0.775 0.873 0.909 0.895 34 ----- ----- ----- ----- ----- ----- ----- ----- 0.704 0.907 0.733 0.848 0.805 0.827 35 ----- ----- ----- ----- ----- ----- ----- ----- ----- 0.826 0.732 0.804 0.784 0.782 36 ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- 0.640 0.818 0.820 0.854 37 ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- 0.854 0.748 0.901 38 ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- 0.800 0.804 39 ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- 0.731 Count 30 17 8 10 12 14 14 15 9 2 7 5 3 3
Now, what do we make of all this? Let's take them one at a time. This first group is guys who debut at age 25, and played for 2 years as a regular. As you'd expect, they had their worst year, on average, in the last (second) year. So, we really don't learn much from this group of players. For players who happened to have played 3 years, they hit their peak in their middle year (age 26), and performed worst in their last year (age 27), which tradition has shown us to be a player's peak age. Strange isn't it? Well, not so strange, when you consider that the player's worst year was his last year. For players with 4 years experience, their best year was age 27, and their worst was again their last year (age 28). For players with 5 years experience, their best year was their FIRST year (age 25), and their worst was their second-to-last (age 28). A slight surprise, but at this point, we are starting to lose our sample size.
As you go through each list, you will see that the longer a player plays, the more opportunity he has to peak later. Think of Edgar Martinez. If your career is over at age 26, how can you peak at age 27? As well, in virtually every class, not only is their last year their worst year, but in a great majority of those cases, the drop-off rate between their last 2 years is far greater than any other 2 years. Again, this is part of selective sampling. Since a manger gets to choose if a player continues to get 300 PAs, a player will not have a chance to show that the previous year, while bad, wasn't as bad as his abilities say it should have been.
The delta approach, with a twist
I will run a delta approach to the original sample of players (Williams out, Raines in), but I will ignore the player's last year. Since it is his last year, is it virtually impossible that a player will have had his peak season at this point? In fact, 14% of the players had their peak year in the LAST year. Remember the lies and stats story? Well, let me give you some more details. A great majority of the players who peaked in the last year also only played 2 or 3 seasons. If we look at those guys with at least 7 years experience, 11 (out of 388, or less than 3%) players peaked in their last year, with Kevin Mitchell being the most prominent of those players.
This is probably a good point to mention that the player stats were unadjusted. There are two important adjustments that should be made: park, and year. A player who manages to switch from Dodger Stadium to Coors Stadium will have his hitting stats go up overall. Therefore, any player who happens to switch parks will not have an accurate reflection of his peak year, if we don't account for this. However, we are not looking at individual players, but players as a group. And you would expect that for every player that goes from a hitting park to a pitching park that you would have a corresponding player go the other way. To be more accurate, you should account for this. But you will not add much accuracy if you start to adjust for park.
The year-to-year changes in stats is more problematic. While we are "saved" in the park adjustments with players being traded for each other, everyone gains if looking at stats from 1968 to 1969. You will find that a disproportionate number of peak years will occur in high-scoring years. This should be accounted for. For this article, let's let that one slide. In a follow-up article I will do on aging, I will not only consider the park and year, but I will bring in a much larger sample of players.
The results
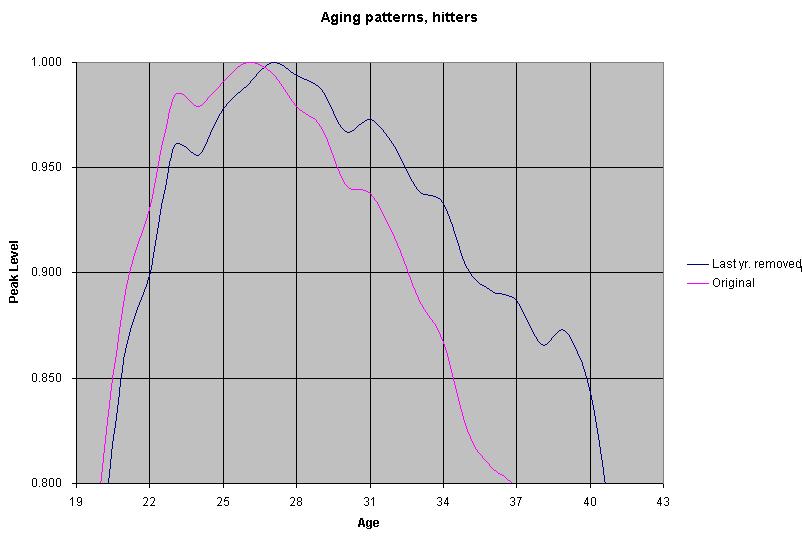
Here's a table showing the aging patterns for the sample of players described. A player's peak age is around age 27, with the age group 23 - 32 being a hitter's 10 best years.
However, with the player's last year not removed, things change slightly. A player's peak age is 26, while his peak career is from age 22 to 30. This is a false representation of a player's aging pattern.
I would not be surprised if there are other considerations that I have not looked at that would push the peak age all the way to 28 or even 29. Or that if I approached this problem from a different angle, I'd get different results. The best way to do this study is to have every MLB player play from age 18 to 48, and give them each 100,000 PA per year. Then we can find the true aging patterns.
Giving each player 500 PAs, and selectively choosing which years they get to perform in to show their abilities is a huge stumbling block. While the effect of selective sampling for a hitter's aging patterns is real, but not very pronounced, the effect on a pitcher's aging patterns is huge. I will look at pitchers aging patterns in a future article.
Aging patterns, hitters Age Count Level Count Level 19 3 0.652 3 0.682 20 9 0.764 10 0.799 21 43 0.863 45 0.891 22 106 0.899 110 0.930 23 196 0.960 212 0.984 24 292 0.956 328 0.979 25 386 0.978 441 0.991 26 450 0.989 516 1.000 27 487 1.000 573 0.995 28 466 0.994 556 0.979 29 423 0.987 515 0.969 30 358 0.967 452 0.942 31 302 0.973 376 0.938 32 233 0.960 313 0.917 33 168 0.939 239 0.888 34 113 0.933 169 0.867 35 74 0.902 116 0.825 36 47 0.891 75 0.807 37 28 0.887 47 0.796 38 15 0.866 28 0.745 39 6 0.872 15 0.726 40 5 0.843 6 0.716 41 2 0.764 5 0.637 42 2 0.641 2 0.546 43 0 0.769 2 0.655 The first level column is with the hitter's last year removed, and the second level column is with the hitter's last year in tact.
June 26, 2002 - Charles Saeger
Interesting stuff. A few questions, since you have the data --
How does a player's individual stats progress? Batting average, home runs, walks, steals, yadda yadda yadda. Does a player who was, say, a high-average player lose more batting average (relative to ability) as he ages? Does he lose more speed?
Is there any change in the rate as the march of time has progressed?
Do some positions age faster than others?
June 26, 2002 - tangotiger
(www)
(e-mail)
In a study I did in March 2001 (which included the hitter's last year, but used a much larger sample of players): hitters improve their walk ratio virtually every year, they strikeout the least at age 29, get their best HR ratio at age 27, their balls in play success goes down almost instantly, their line drive power stays pretty flat for a long period of time, their speed as measured by triples goes down instantly, their speed as measured by SB peaks at 24 and goes down almost at the same rate as the triples.
My intention is to eventually re-run that study but with the new information I've discovered recently regarding the last year effect.
A thread with all the data can be found here - http://baseball.fanhome.com/forums/showthread.php?threadid=662692#post1958322
June 26, 2002 - tangotiger
(www)
(e-mail)
As to your other question on different aging patterns for different types of players, I also took a look at this a while ago. My sample set was pretty small, and so, I wouldn't want to make any strong conclusions based on it, but the evidence was showing that all types of players age the same way. The Tim Raines class of runners would lose his abilities across the board (SB, HR, Hits) to the same extent that the Wade Boggs class of runners would. This is another area that I will be (eventually) looking at.
June 26, 2002 - Dan Turkenkopf
(e-mail)
Very interesting...
I'm wondering if the peak age has shown any change across time - or if the different aspects you discuss in your response to Charles have been affected differently by era.
For example, does power (represented by homers) drop off slower in a live ball era than a dead ball one - or today due to improved conditioning and the increased importance of the long ball?
I know the sample size is probably too small to make that determination, but if you have any insights, I'd love to hear them.
June 26, 2002 - tangotiger
(www)
(e-mail)
I usually only look at 1919 and later because I don't think that "power" is well-represented in the pre-1919 time period. Even HR are not true representation of "power", but it's still pretty good to use.
In that March 2001 study (which I'll reiterate used a slightly different methodology), I found virtually no difference between the aging patterns of the various skillset between 1919-1979, and 1979-1999.
In that study, I concluded the following: "...the historical averages match up very well with the recent period. While today's ballplayers may be better, and playing longer, the "curve" of their aging is the same. There is no age bias with today's regimen of training and medication. It affects all age groups the same."
June 26, 2002 - jmac
As alluded in the (I believe) 1982 Abstract, in attempting the follow aging patterns using only hitting stats, you are dealing (after age 30 anyway) with a continually more & more skewed group of players, e.g. those players whose hitting stats DON'T decline with age as fast as the average player. Because if they did, they wouldn't be in the league.
June 26, 2002 - tangotiger
(www)
(e-mail)
jmac: yes, I agree that you have other forces at work. This is why I first presented that large chart breaking up the performances by number of years in the league (for players debut at age 25).
What I can do is present a similar chart for players debut at age 22, 23... etc, so that we can determine a more specific pattern. The only reason I did not do so is that it would be so overwhelming that the reader wouldn't know where to begin. As well, this kind of analysis suffers from sample size issues, and so conclusions will not be reliable. Let me think how I can best present such data.
June 27, 2002 - Gerry
"Age is calculated as of July 1st, with the remainder rounded off."
In other words (and more simply), age is calculated as of Dec 31st.
"One standard deviation means that 68% of all results will fall within .500 +/- .016 probability."
Only because you are sampling from a normal distribution (or a binomial distribution with such parameters as to make the normal distribution a good approximation). Do you know that batting averages or LWR or whatever follows a normal distribution?
"I will define a regular player as someone who has at least 300 PA (AB+SF+BB+HBP) in a season."
Do you stick to that in strike years, when 300 PA were harder to come by? Do you use that same standard for 154-game seasons and for 162-game seasons?
June 27, 2002 - D Smyth
Tango hits the big time! Good stuff. An interesting type of study to do, because the actual calculations are very simple--the player's age, PA total, and hitting rate. The whole issue of the study is identifying and dealing with the sampling problems, as Tango takes the time to discuss. I do think the league and park adjustments should be done, so that there is more confidence in the conclusions. I look forward to the followup article.
June 27, 2002 - tangotiger
(www)
(e-mail)
In other words (and more simply), age is calculated as of Dec 31st.
I was wondering when someone would say that. Yes, I simply make Age = Year - YOB . Not only is it a snap to calculate, you also don't need to know them month the player was born.
Do you know that batting averages ...follows a normal istribution?
I seem to recall looking at this a long time ago to determine how many single-hit and multi-hit games a player would have, if it did follow such a distribution. And it did.
Do you stick to that in strike years, when 300 PA were harder to come by?...
Yes, on all counts. It's not as if I can say that the reliability of 300 PA in 1982 is similar to 200 PA in 1981. 300 PA is 300 PA. In the cases like this, my sample size goes down somewhat. My other option would be to limit my sample set so that 1981 is not part of the study. I can do this for pairs of seasons, but at the extent that I looked at this issue, I needed to have 5 and 10 and 15 consecutive years. Removing 1981 from such a study would drastically reduce my sample size. Your point is valid however.
I do think the league and park adjustments should be done, so that there is more confidence in the conclusions.
I agree. As my sample size goes down, these adjustments become much more important. As for followup articles, I think I'm going to have to make it a whole series of them because there are so many results that this dataset will give us.
June 27, 2002 - Ben Vollmayr-Lee
Nice work Tango.
I missed where the confidence levels come in. But in reponse to Gerry's comment: for applications where you are determining the confidence level of the mean (say, average OPS of 30 year olds), you do not need the distribution of OPS to be normal. The reason is the "central limit theorem" which basically says that means are normally distributed (once the sample is big enough) even when individual variables are not. This is a very powerful theorem and is basically the foundation of the field of statistics.
June 28, 2002 - Gerry
Ben Vollmayr-Lee wrote,
...for applications where you are determining the confidence level of the mean (say, average OPS of 30 year olds), you do not need the distribution of OPS to be normal. The reason is the "central limit theorem" which basically says that means are normally distributed (once the sample is big enough) even when individual variables are not. This is a very powerful theorem and is basically the foundation of the field of statistics.
Even a theorem as powerful as The Central Limit Theorem has hypotheses, though, and is only valid when those hypotheses are satisfied. I don't think this is the place to get into the details. Let's just say you have to know *something* about the distribution of the variables whose mean interests you - it's not a blanket statement about everything, all the time.
June 28, 2002 - tangotiger
(www)
(e-mail)
One of the previous posters mentioned that players who play longer will have different aging curves than those who don't.
Working always from the same sample, I broke my main sample into three subsets. The first subset is those players who play between the ages of 24 (or earlier) and 33 (or later). This is a group of players that have at least 10 years experience, and who have had the chance to play during the "traditional" peak years. The second sample are those players whose career was over by the age of 31. Therefore, these might be those guys who you think might have peaked earlier. The third sample is everyone else. This means, it's a group of players whose career was over after the age of 31. These are just a whole bunch of different types of guys, but skewed slightly towards the older players.
Because of sample size issues, some of the results might look strange. In any case, here it is:
Age # Long # Short # Rest 19 2 0.565 1 0.810 20 5 0.687 4 0.871 21 25 0.816 15 0.921 3 0.936 22 61 0.857 36 0.939 9 1.025 23 99 0.930 81 0.999 16 1.007 24 140 0.936 131 0.987 21 0.972 25 140 0.982 167 0.994 79 0.929 26 140 0.989 191 0.994 119 0.973 27 140 1.000 181 1.000 166 0.991 28 140 0.987 141 0.994 185 0.989 29 140 0.981 80 0.966 203 1.000 30 140 0.979 218 0.969 31 140 0.977 162 0.980 32 119 0.954 114 0.976 33 88 0.938 80 0.951 34 58 0.930 55 0.945 35 39 0.885 35 0.930 36 27 0.887 20 0.905 37 17 0.856 11 0.937 38 11 0.842 4 0.906 39 5 0.809 1 1.014 40 4 0.790 1 0.942 41 2 0.672 42 2 0.563 Hopefully, the formatting comes out here.
What do we see? As you would expect, those players with long careers centered around the expected peak years did just that. They had their best years at the 25-29 level, peaking at age 27. They had a bit of a jump prior to that. Then they had a slowly declining phase to age 34, after which they plummeted. However, don't forget we specifically selected our subset for players who played between the ages of 24 and 33. Therefore, we should not be surprised to see demarcation points close to these ages. Furthermore, the peak point was still age 27. The slowly declining phase is a result of the selective sampling.
The second set of players is far more interesting. These are players, for whatever reason, had their careers over by the age of 31. These players did not have the traditional aging curve. Essentially, they stayed at a peak level between the ages of 23 and 29. Is it possible that there is a class of players that don't get to the next level? That perhaps, there is a class of players that peaks at age 23 and stays there? Or is this again a bias in our sample? That because we specifically chose our players whose careers ended prior to age 31 then this is exactly what we expected to see? This is a much more likely result. Management did not give the players a chance to show their stuff, and simply cut them before their truly good seasons could be shown.
The last set of players has a bias to be an older type of player, and the results show this. These players peaked between the ages of 26 to 32, peaking at age 29.
Selectively choosing your sample set leads to many biases.
July 1, 2002 - F James Mohl
Do you feel the Linear Weights Ratio is a much better measure of offensive performance than OPS? If so, what evidence do you have? If not, may I suggest you use OPS+ in your future studies? Not only will this take care of the adjustments for park and year which you indicate are necessary, but it will make it easier to incorporate your findings with other studies that are OPS+ based. In fact, if you use Baseball Reference data, you will have available not only OPS+, but BA+, OBP+ and Slg+ (and, indirectly, Isolated Power+), so you can easily determine if different skills decay at different rates.
July 1, 2002 - tangotiger
(www)
(e-mail)
Do you feel the Linear Weights Ratio is a much better measure of offensive performance than OPS? If so, what evidence do you have? If not, may I suggest you use OPS+ in your future studies? On June 26, I posted the following on fanhome "[OPS]'s extraordinarily useful and practical because: - it's readily available - it's made up of the two most important rate stats we have - it's highly correlated to runs scored - it can be used in research when you have the power of sample size that masks its deficiencies
It is NOT useful because: - you can not count on it for game-level decisions - you can not count on it to evaluate players of weird profiles - it does properly weight all the events
So, depending what you are trying to do, OPS is either a godsend or a bane.
The reason I hate it is that people use it for the exact reasons that it is not useful."
In sum, OPS is used as a stand-in when you don't have something better. LWR is something better.
I'm not sure why I need to show "better" evidence to use LWR over OPS. All the deficiencies of OPS are taken care of in LWR. I can use LWR to convert it into Runs Created or Runs over average, or really anything, in a simple one-step process. LWR is the best "rate" measure we have. (If you want more discussion on LWR, you can check out my site at http://www.geocities.com/tmasc/lwr.html which will give you the full formula, as well as a link that discusses LWR.)
******** Not only will this take care of the adjustments for park and year which you indicate are necessary, but it will make it easier to incorporate your findings with other studies that are OPS+ based...
I have the data to calculate the park/year adjustments, I just didn't want to add another layer of complexity. (If someone wanted to reproduce the above research, they could. If I added park and year adjustments, they couldn't.) As I indicated, I'll add that layer the next time. All studies that are OPS+ based are flawed for the reason that they rely on an indicator that has deficiencies that are circumventable.
July 3, 2002 - Ed
Wading into the Ben-Gerry discussion of normality, I was curious, so I performed the Shapiro-Wilk test of normality on batting averages, by season, including in each season those players with 300+ PAs.
Three numbers are shown here, year, # of players with 300 PAs, and the observed p-values for the Shapiro-Wilk tests. You can see that whether one is willing to conclude that the seasonal results are normally distributed overall depends on what level of significance will be tolerated. [The null in the S-W test is normality].
1960 126 0.736 1961 151 0.030 1962 168 0.293 1963 166 0.233 1964 177 0.961 1965 173 0.899 1966 169 0.161 1967 168 0.271 1968 163 0.635 1969 194 0.085 1970 210 0.721 1971 206 0.183 1972 195 0.060 1973 222 0.968 1974 216 0.353 1975 215 0.689 1976 211 0.181 1977 236 0.171 1978 224 0.623 1979 231 0.732 1980 237 0.246 1981 154 0.535 1982 225 0.920 1983 242 0.516 1984 231 0.709 1985 224 0.176 1986 234 0.013 1987 236 0.320 1988 228 0.072 1989 231 0.072 1990 233 0.503 1991 226 0.861 1992 241 0.053 1993 244 0.346 1994 206 0.023 1995 224 0.153 1996 249 0.855 1997 244 0.187 1998 261 0.915 1999 276 0.781 2000 256 0.874 2001 260 0.581
July 4, 2002 - Ben Vollmayr-Lee
Okay, there's a lot of confusion here on the BA distribution question, and I contributed to it, so let me try to straighten it out. Pulling no punches (but all meant in good fun), and going chronologically
Tango's confusion: his poll example was a perfect use of the central limit theorem. But his application to how a batter's BA over 600 AB is related to their 'true' BA ability wasn't perfect. If the batter has the same chance of a hit in each of their AB then the CL theorem would apply. But the batter doesn't. As it turns out, neglecting this issue and blindly applying the CL theorem is a reasonable thing to do anyway, but it requires some motivation and is not explained by the poll example. Bad Tango.
Gerry's confusion, part I: might not have existed. He asked "Do you know that batting averages ... follows a normal distribution?" If he was thinking that the issue is whether the distribution of batting averages around the league is normal, then he missed Tango's point. But if he was thinking "do you know that a player's actual 600 AB batting average is distributed normally around their 'true' batting average?" then he was asking exactly the right question.
Ben's confusion: I thought Tango was applying confidence levels to, say, the average BA of all 27 year olds. Here the CL theorem would apply: the average BA taken from N players is a normal distribution provided that N is big enough. I qualified my statements correctly, but of course this had nothing to do with Tango's argument, so my reply to Gerry was a non-sequitor and way purple.
Gerry's confusion, part II: instead of calling me on my non-sequitorarity (see, I like pizza), he questioned the hypotheses of the CL theorem. For what it's worth: the conditions for the CL theorem to apply are simply that the original distribution needs to have a non-infinite standard deviation, and N independent samples have to be drawn from this distribution, with N "big enough" (for realistic applications, 20 gets you in the ballpark and 100 is damned accurate). The problem with Tango's use of the CL theorem with BA is that the samples are drawn from different distributions: a batter's chance of a hit against Randy Johnson is different than it is against Livan Hernandez. And Bob Brenly is happy about this.
Ed's confusion: probably induced by the mess that preceeded him, he thought the issue was distribution of batting averages around the league.
I hope this is taken as lightly as intended and no one is offended. Or failing that, I hope I offended everyone equally so as to be democratic about it. Now for the argument why Tango's analysis of confidence levels for BA is reasonable:
Instead of having 600 AB with a chance 'p' of getting a hit each time, a more realistic model is that a batter has some 20 AB with a chance 'p1' and another 35 AB with a chance 'p2', another 20 with a chance 'p3', etc. (these could come by ranking the toughness of the pitchers and throwing in a Coors factor, for example). The CL theorem can be applied to each of those sub-samples, with each of their 'p' values and N, but that doesn't tell you yet much about what to expect for the combined average. However, two things work to your advantage:
1) the std dev of the 2-case distribution (hit or not-hit) is not strongly dependent on the probability 'p' away from the extremes of 0 and 1. The std dev is sqrt(p*(1-p)), so you get .433 for p=.25, and .477 for p=.35. They fall within 10% of each other, and if your end conclusion is that a .300 hitter is .300 +- .010, you're only working to 10% accuracy simply by rounding the .010 to the third decimal place. So we can approximate the std dev for each of the sub-sample means by just using the overall rate 'p' (Note that if the p1, p2, ... vary between .25 and .35, you're doing much better than 10% accuracy when you average together the subsamples, because both end points are within 5% of the middle. Even to get 5% accuracy you would need all cases to be extremes, in reality they are spanning the spectrum and even more likely to be in the middle, so we're talking 1-2% accuracy)
2) these different distributions with their own p1, p2, etc, have N's much smaller than 600 AB in their sqrt(p*(1-p)/N) (the std dev of their AVERAGE), so how can we justify using sqrt(p*(1-p)/600) as the std dev for the combined average? The reason is because each sub-sample average is independent of the others, so when combining them the errors tend to cancel to some degree. This is the same effect that makes the CL theorem work to begin with, we're just doing a more complicated version of it this time.